Complex numbers are an essential extension of the familiar real number system, allowing for the expression and manipulation of numbers that are not confined to the real number line. The concept of complex numbers was developed to solve equations that do not have solutions within the realm of real numbers, particularly quadratic equations with negative discriminants.
A complex number is typically written in the form z = a + bi, where:
a and b are real numbers.
i is the imaginary unit, defined by the property i² = −1.
In this form, a is known as the real part of the complex number, while b is referred to as the imaginary part. The term "imaginary" does not imply that these numbers are any less real in mathematical significance; rather, it distinguishes them from real numbers and highlights their unique properties.
The set of all complex numbers is denoted by C. This set encompasses all possible numbers of the form a + bi, where a and b range over all real numbers.
Complex numbers can be visualized on the complex plane, a two-dimensional plane where the horizontal axis represents the real part and the vertical axis represents the imaginary part. This geometric representation helps in understanding operations on complex numbers, such as addition, subtraction, multiplication, and division.
Addition and Subtraction: Complex numbers are added or subtracted by combining their real parts and their imaginary parts separately.
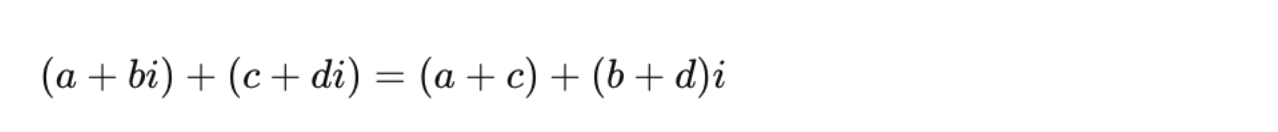
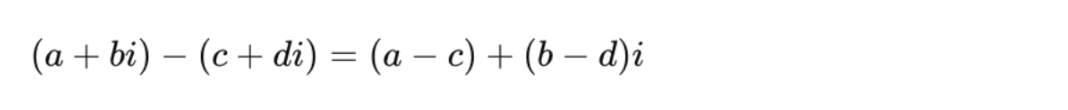
Multiplication: The product of two complex numbers involves distributing the terms and applying the property i² = -1.
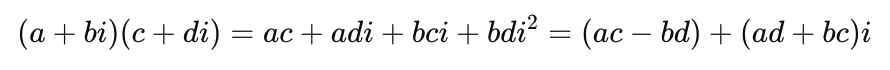
Division: Dividing complex numbers requires multiplying the numerator and the denominator by the conjugate of the denominator to rationalize it.
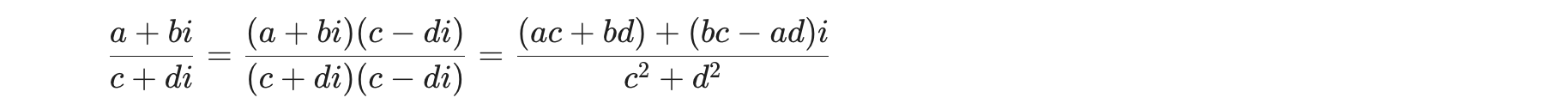
The complex conjugate of:

The modulus (or absolute value) of a complex number z is given by:

The modulus represents the distance of the complex number from the origin in the complex plane.
Complex numbers have profound applications in various fields of science and engineering, including electrical engineering, quantum physics, applied mathematics, and control theory. They are also fundamental in the study of more advanced topics such as complex analysis, Fourier transforms, and signal processing.
In summary, complex numbers enrich the number system, providing powerful tools to solve equations and model phenomena that are not adequately addressed by real numbers alone. Their study opens up a vast and intricate mathematical landscape, offering deeper insights into both theoretical and practical problems.